１ 三坐標測量簡介

   三坐標測量機是一種通用性強、自動化程度高 的高精度測量系統。對一般的測量軟件而言，三坐標測量機的測量過程，可分為以下幾個步驟（假設測頭校驗與坐標系的建立已經完成）。 

（１）采集特征點的坐標位置。即通過測頭直接觸測被測對象、 讀取并記錄坐標值。

（２）按照“最小條件”對前面測得的特征點進行計算與構建。如果是形狀誤差，可直接計算出誤差值。 

（３）如果是位置誤差則按照“最小條件”將特征點構建出誤差評價所需的點、線、面等基本要素，并用數學的方法計算出各要素間的實際誤差，對照圖紙判斷其是否合格。 在這一過程中，第一步特征點的采集是后續工作的基礎，如果有誤，構建出的特征要素就不能真實的反映出零件的實際情況，誤差計算與評價的結果也就不可信了。因此，特征點的位置、特征點的數量和采集方式對三坐標測量結果有著非常重要的影響。本文就是針對此類問題，對三坐標測量的取點進行了一定程度的實驗與討論，并得出了有益的結論。

２ 平面度測量與評價方法 
   平面度測量是幾何量評價的基本內容，是１４類 誤差測量（直線度、平面度、圓度、圓柱度、線輪廓度、面輪廓度、平行度、垂直度、傾斜度、同軸度、對稱度、位置度、圓跳動、全跳動）中最基本也是最具有代表性的。按照“最小條件”的要求，平面度誤差可以由最小包容區域法、對角線法和三點法來評定。以最小包容區域法為例，只要滿足了下列條件中的一條，即可確定平面度誤差的大小：
（１）三角形法則。圖１（ａ）為三角形法則。圖中點A為凹形實際表面的最高點，a、b、c為３個最低點，A點的投影落在由a、b、c這３點構成的三角形內。在滿足這一條件的基礎上，a、b、c點確定平面１，過A點做平面２平行于平面１，則平面１與平面２之間，就構成了最小區域，兩平面間的距離即為平面度誤差。

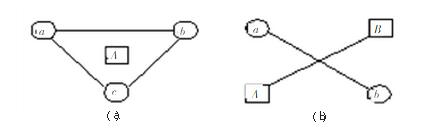
（２）交叉法則。圖１（ｂ）為交叉法則。圖中點A、點B為鞍形實際面的最高點，點a、點b為最低點，過直線AB和過直線ab決定了一對平行平面，且兩直線成交叉狀態，則兩平行平面就構成了最小區域，兩平面間的距離即為平面度誤差。
對三坐標測量而言，上述兩種評價方式，都是由相應的特征點（最高點和最低點）通過計算得到的，可以這樣講，特征點的位置與數量，實際決定了平面度誤差的大小。
另外，評價每一種要素都有一個最低測量點數，如：平面度測量，無論采用哪種法則，都至少要測４點，才能計算平面度誤差；直線至少要測３點；圓至少要測４點；圓柱至少要測６點。一般情況下，如果測量條件與對象已經確定，那么測點越多，測得的誤差值就越能反映測量對象的真實情況，但考慮到測量效率和經濟性，測點不可能無限制的增多，特別是在某些精度與批量都要求比較高的場合，希望能夠找到一個合適的測點數，使得測量設備既能較快地完成測量任務，又能較為真實地反映被測對象的實際情況。
3 總結 

三坐標測量機作為一種全新的測量方式，已經 被越來越多的用戶所接受和肯定，但由于測量原理的不同，該測量設備有其獨特的測量規范。

在三坐標測量中，首先要對特征要素選擇合適的測點數，測點數過少，會造成較大的誤差；對于確定的測量對象，可以通過樣本實驗尋找合適的測點數（這對于批量的高精度測量更有意義），以保證測量的精度與效率；比較各類表面，精度高的表面獲得的測值，比精度低的表面獲得的測值更為可信，測點數對其影響也更小；手動取點誤差大，應選用自動測量的方法。采點是三坐標測量的基礎工作，為保證測量結果真實可信，應予充分重視。不論是形狀誤差、還是位置誤差，或者尺寸的測量，有了正確的測點信息，才能保證計算評價的真實性。